当算法与前端相遇

前端需要了解算法吗？读了几章《算法导论》，结合一下项目实践试着以前端的视角来窥视一下算法的世界。

算法与前端

和一些同事闲聊过前端是否有必要研究算法，多数人给出了否定的答案，他们的理由是：

一、浏览器能调用的资源比较少，注定处理不了很多数据，算法优化效果不明显；

二、前端只处理页面逻辑，很少需要特别设计复杂的算法。

本着小马过河的精神早就想研究一下算法这个大宝贝儿，前段时间终于遇到了这样一个契机，由于工作的原因需要写一些稍微复杂一点的页面程序，写的感觉比较吃力，于是读了几章《算法导论》，觉得确实有必要拿出来分享一二。先给出前端有必要学习算法的三条理由：

一、资源少更需要优化；

二、前端承担的业务和交互会越来越复杂，做一些平台和组件的时候需要借助算法设计，下面会给出两个前端算法的例子；

三、熟悉算法的一些套路可以提高设计代码和读懂代码的速度，减少bug。

算法的概念

描述一个特定的计算过程来实现输入和输出关系。

算法设计

算法设计的目的是证明输入和输出满足某种关系，最常用的两种设计思路就是循环和分治。下面分别介绍设计技巧：

循环

先给一个经典的插入排序示例：

插入排序算法描述：

起始：从第二个开始；

保持：向后遍历每个元素，记录当前元素并将当前元素和前面的元素相比，如果前面元素比当前元素大就向后移动一位，并记录移动后的空缺位，直到遇到比当前元素较小的元素或者到达左边界，将当前元素放入记录的空缺位中，然后下一个；

终止：最后一个元素。

// 插入排序核心代码
for (var i = 1; i < array.length; i++) {
    var key = array[i];
    var j = i - 1;
    while (j >= 0 && array[j] > key) {
        array[j + 1] = array[j];
        j--;
    }
    array[j + 1] = key;
}

Demo

循环相对递归要简单一些，任何循环都能拆成上面三步，但是每一步中可能会包含另一个循环或递归，设计算法的时候可以先设计最外面的三步，然后推敲每一步的分支逻辑和设计每一步的具体实现(具体实现可能要嵌套其他算法设计)。

递归(分治)

递归是将原问题分解为几个更小但类似于原问题的子问题，然后递归解决这些子问题，最后合并这些子问题的解产生原问题的解。我们同样以一个示例作为开始 --- 快速排序：

快速排序算法描述：

分解：将数组的最后一个元素作为分割元素，移动数组中的元素，使左边小于此元素右边大于此元素，将此元素的左右两部分视为新的数组；

解决：最后被分割而成的数组长度为0和1时直接返回，为2时排序；(为3时继续分解)

合并：无(由于数组是址引用，每次都是原址排序，所以不需要单独的合并操作)。

// 快速排序核心代码
function quickSort(array, from, to) {
    // 参数容错，可使初始化不用做特殊处理
    from = from || 0;
    to = to === undefined ? (array.length - 1) : to;
    // to || (array.length - 1); 此种写法对 to=0 的情况会出问题

    if (from < to) {

        var markIndex = from - 1;  // 标记位
        var spaceItem = array[to]; // 默认最后一个

        // 找出分水岭的位置，并把大小数分列两侧
        for (var i = from; i <= to; i++) {
            if (array[i] <= spaceItem) {
                markIndex++;
                var temp = array[markIndex];
                array[markIndex] = array[i];
                array[i] = temp;
            }
        }

        arguments.callee(array, from, markIndex - 1);
        arguments.callee(array, markIndex + 1, to);
    }
    return array;
}

在具体实现上我们采用一种驱赶贪吃蛇的策略来分解问题，markIndex作为贪吃蛇左起点的标记位，初始化时贪吃蛇没有长度，所以将标记位标记为from - 1(最开始时是-1，子问题也满足逻辑)；把数组(或数组的片段)最后一个元素当做分割元素spaceItem；然后从左到右遍历数组(或数组的片段)，如果当前数小于或等于spaceItem，那么将当前数和贪吃蛇的左边第一个数互换位置，使贪吃蛇向右移动一位，相应的markIndex也加1，如果当前数大于spaceItem，那么贪吃蛇向右涨一位。补充一下如果数组(或数组的片段)第一个元素小于spaceItem，会原位交换(markIndex==i==0)，这本身是没有意义的，但是如果加判断来消除这个逻辑分支，会带来两个问题，1、代码变复杂了，2、多数情况是非原位交换，每次都判断反而计算量更大。

为什么要把最后一个元素作为分隔元素，而不是第一个呢？因为如果将第一个元素作为分隔元素会在从左到右的比较和交换中失去位置的控制，而用最后一个元素作为分隔元素再使用小于等于的判断条件可以取巧分隔数组。

Demo

前端算法示例

循环依赖的判断

这是从实际项目中抽象而出的一个例子(由于公司的保密规定具体项目信息就不方便透露了)，对处理一些任务依赖、前端模块依赖等问题上有一定的通用性，下面是一个依赖示意图：

A --> B --> C --> D
      ∧     |     |
      |     ∨     | 
G <-- F <-- E <───┘

描述节点的部分数据如下：

[
    {
        "resourceId": "sid-E312C067",   // 节点标识
        "stencil": {
            "id": "start"
        },
        "outgoing": [
            {"resourceId": "sid-6A757572"}
        ]
    },
    {
        "resourceId": "sid-6A757572",
        "stencil": {
            "id": "bind"
        },
        "outgoing": [
            {"resourceId": "sid-C92FBDAE"}
        ]
    }
]

第一个例子是较为简单的判断是否有依赖关系，下面是算法描述：

分解：首先找到开始节点，以开始节点为起点，路径记录为空数组，遍历当前节点 outgoing 属性中的元素，通过元素的resourceId查找节点进入子问题；

解决：记录当前节点从起始位置到当前节点之前的路径，如果当前节点的resourceId出现在了路径中，那么就出现了循环终止问题分解向上返回结果；如果当前节点的resourceId未出现在路径中，那么继续向下分解；

合并：如果出现“已出现循环”的结果，将此结果层层向上返回；否则遍历全部节点，向上层层返回默认值“未出现循环”。

Demo，可在控制台查看代码。

非对齐表格

先看结果：

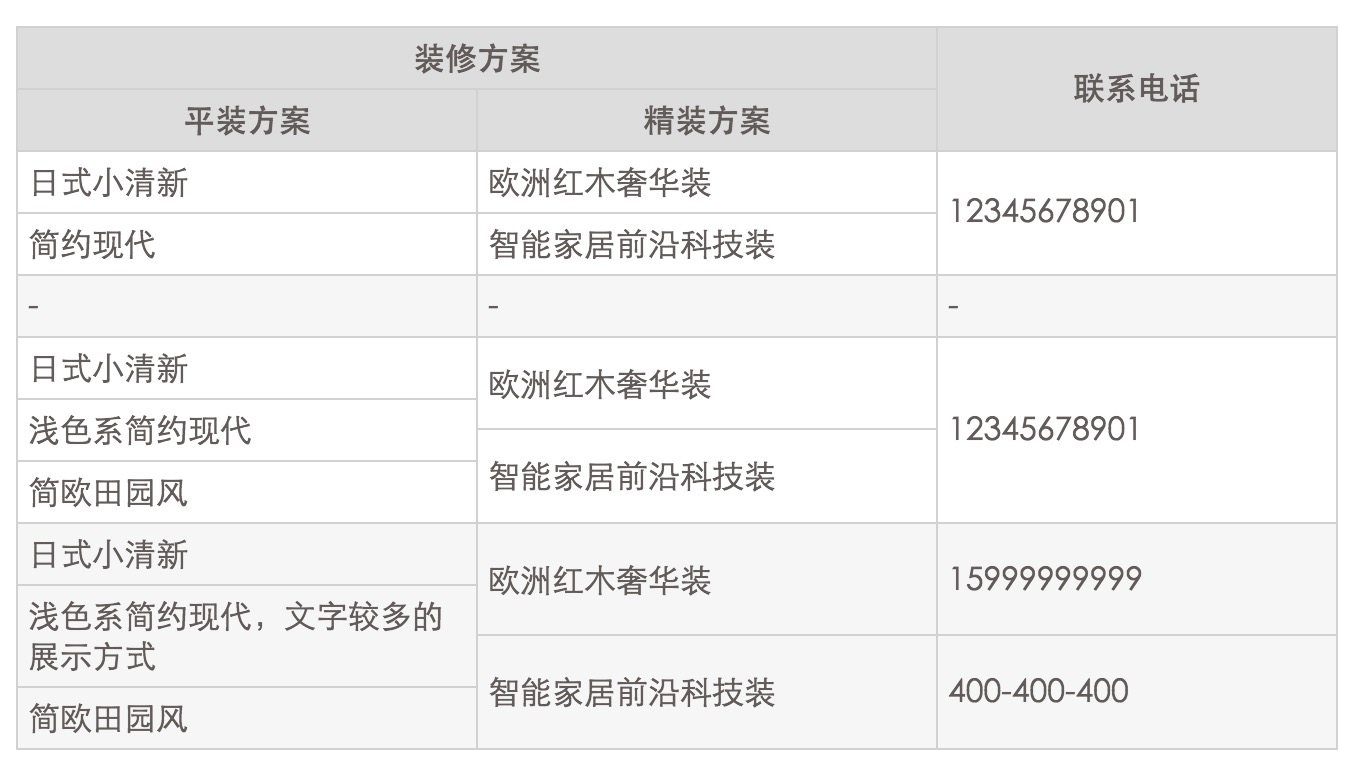
特点：如上图，一行中的列不是对齐的，有子列的存在，子列间横向不对齐数目不固定。

使用场景：将对象以表格的形式展现。

功能说明和实现描述：如上图这个示例的功能就是将数据已表格形式来展现，数据展示上表头配置优先，如果表头中未配置数据列那么数据不展示未配置列，不支持自适应宽度，每个子列(最末端的才生效)设置固定宽度，最后返回表格的 html 字符串，表头配置代码和调用方法如下：

// 表头配置方法
[
    {
        key: 'shopName',
        title: '公司名称',
        width: 200
    },
    {
        key: 'plan',
        title: '装修方案',
        children: [
            {
                key: 'commonPlan',
                title: '平装方案',
                width: 230,
                isWrap: true
            },
            {
                key: 'exquisitePlan',
                title: '精装方案',
                width: 230,
                isWrap: true
            }
        ]
    }
]
var html = objectToTable(seniorData, seniorDataHead);

在实现上表格是由 div 拼接而成，拼接被分成两部分：第一部使用递归遍历表头的设置，生成各列的宽度，其实主要是将子列的宽度累加得到父列的宽度，顺便将表头的 html 生成出来；第二部分使用前一步生成的表头设置再结合数据生成表格数据部分。 在样式上采用 flex 弹性布局来处理容器等高内容项不等高的均分问题。

表头部分算法描述：

开始之前：表头的配置要求是一个数组，为了逻辑上的归并和特殊处理最外层，我们将用户传入的表头设置加工成如下格式：

{
    key: '$root',
    children: tableHeadConfig
}

分解：如果当前字段的配置有 children，表示当前字段有子字段，需要表头嵌套，然后遍历 children 并将其每一个子项作为下一个子项的传入参数。

解决：如果当前字段的配置没有 children，那么说明已经到了最底层，拼接当前所需的 html 片段并处理当前列的宽度(读取用户配置或者采用默认设置)，以对象的形式返回这两个值，格式如下：

var result = {
    html: '...',
    width: 130
};

合并：累加遍历 children 得到的每一个 result.width 作为当前列的宽度，生成一个叶子节点作为嵌套列的头；再用一个class为row的容器盛放result.html字符串拼接结果，作为嵌套列的分列；最后用一个class为column容器盛放嵌套列的头和分列。

表体部分算法描述：

开始之前：数据要求是一个数组，为了逻辑上的归并和特殊处理最外层，我们将用户传入的数据加工成如下格式：

{
    '$root': data
}

分解：由于表头配置优先，所以分解依然是按照表头设置的数据来层层分解，不同的是分解到每一列时需要找相对应的数据，如果没有找到对应数据需要补一个空数据占位并且不再向下分解当前列。

解决：到达表头的叶子节点后，展现数据的html片段的拼接方式要根据数据类型来确定，如果数据类型是数组，就要按多行呈现的方式来拼接，如果是非数组的数字或字符串那么直接输出叶子节点的拼接结果即可。

合并：用一个class为row的容器盛放 遍历表头 children 得到html字符串拼接结果，再返回加工后的 html。在数据呈现中不需要展现嵌套列的头，但是嵌套关系需要体现方便布局和后续可能的处理。

Demo。

递归的技巧

在设计递归算法和阅读递归的代码时，要把握的第一个关键就是怎样将入参转化为下一轮调用的入参，这个转换的逻辑就是将大问题转换成较小问题的逻辑；第二个关键点就是入参和出参的设计上，先不要管过程怎样实现将你需要的出参列出来，然后设计入参，在层级逻辑比较复杂的递归中入参最好设计为一个对象，除了要处理的数据本身还有一些上下级的逻辑关系需要传递下去。

一个问题

当两个逻辑可以在一个递归中实现时，是用一个递归实现两个逻辑以提高速度，还是分两次递归使逻辑较为清晰？

时间复杂度

一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。时间复杂度的衡量指标是总运算次数表达式中受n的变化影响最大的那一项。

举几个不同复杂度的例子:

复杂度为 O(n)

手动反转一个数组

function reverse(array) {

    if (Array.isArray(array)) {
        var length = array.length - 1;               // 1
        array.some(function (item, index) {          // n/2
            // 交换顺序
            if (index < length - index) {            // 1
                var t = array[index];                // 1
                array[index] = array[length - index];// 1
                array[length - index] = t;           // 1
            }
            // 结束循环
            else {
                return true;
            }
        });
    }
    return array;
}

// 整体运算量: 1 + (1 + 1 + 1 + 1)n/2 = 2n + 1
// 所以复杂度为:O(n)

在列举其他复杂度的例子之前，我们有必要再引入两个概念: "最坏情况时间复杂度" 和 "期望时间复杂度"。"最坏情况时间复杂度"是处理固定数量的数据时最多运算多少次，比如排序给的是逆序的数据，还有你希望查询的数据在查到最后一个时才出现; "期望时间复杂度"(其中的"期望"是统计学中的一个概念大体相当于平均概率)是处理固定数量的数据时平均运算的次数，上面数组反转的例子"最坏情况时间复杂度" 和 "期望时间复杂度"是完全相同的，对于大多数算法这两个指标通常是相同的，在评估计算量时可能需要区别这两种时间复杂度，但将系数取出后得到的时间复杂度表达式通常是相同的(有一些算法的最坏情况时间复杂度和期望时间复杂度是不同的，比如快速排序)。设计符合期望时间复杂度的测试数据和计算其复杂度需要一些概率基础。

复杂度为 O(n^2)

插入排序

// 核心代码,期望时间复杂度
for (var i = 1; i < array.length; i++) {
    var key = array[i];
    var j = i - 1;
    while (j >= 0 && array[j] > key) {    // 平均概率下,在中部找到自己的位置
                                          // 1/2 + 2/2 + ... + j/2 + (n-1)/2
                                          // = (1 + 2 + 3 + ... + n - 1) / 2
                                          // 最坏情况只要把最后的除2去掉就可以
        array[j + 1] = array[j];
        j--;
    }
    array[j + 1] = key;
}

等差数列的求和公式: n×a1 + n×(n-1)×d/2，代入到上面得

(1 + 2 + 3 + ... + n - 1) / 2
= [(n - 1) + (n - 1)×(n - 2)×1/2]/2
= (n^2 - n)/4

所以插值排序的期望计算量可以简单表示成为: (n^2 - n)/4，最坏情况计算量需要乘2: (n^2 - n)/2，那么插值排序的时间复杂度就可以表示为: O(n^2)。

复杂度为 O(nlgn)

快速排序

快速排序采用递归分割数组，在代码上直接标注计算量比较困难(难点在于确定分割的期望次数和每次分割的计算量)，所以我们需要从另一个侧面来计算快排的算法复杂度。

在快排中每两个元素最多被比较一次，建立随机指示器 X[i,j] = I{z[i] 与 z[j] 进行比较}，(其中中括号中的字母表示下标)，这样算法的总比较次数可以标示为: X = 从1到n-1变量为i求和于 从i+1到n变量为j求和于 X[i,j]。其中 z[i] 与 z[j] 需要比较的概率就是他们在同一分段中被选为主元的概率，也就是 2/(j-1+1)，通过调和级数的放缩再舍去欧拉常数，上面的二重求和最终的计算结果就是 nlgn。